Свойства площади

Площадь фигуры является неотрицательным числом.

Площади равных фигур равны.

Если фигура разделена на две части, то площадь всей фигуры равна сумме площадей образовавшихся частей.

За единицу измерения площади принимается площадь квадрата со стороной, равной 1 единице длины.

Другими словами, площадь квадрата со стороной, равной 1 единице длины, равна 1 единице площади, или 1 квадратной единице. Например, площадь квадрата со стороной 1 метр равна одному квадратному метру

Фигуры, имеющие равные площади, называются равновеликими.

Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не измениться.

Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).

Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол

Отношение площадей подобных треугольников равны квадрату коэффициента подобия.

Медиана треугольника делит его на два равновеликих треугольника.

Отрезки, соединяющие точку пересечения медиан треугольника с вершинами, делят треугольник на три равновеликих треугольника

Средние линии треугольника площади S отсекают от него треугольники площади 1/4 S.

Медианы треугольника делят его на 6 равновеликих треугольников.

Работа над ошибками по теме "Системы уравнений"

Ребята, работу над ошибками выполните в рабочих тетрадях по алгебре. На проверку тетради сдайте 3.12.14. Удачи. И.А.

Ребята, пополните свои справочники по геометрии этим материалом. Для любителей геометрии приведены доказательства утверждений.

1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.

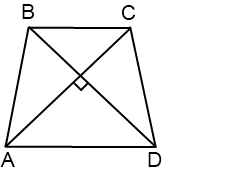
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.



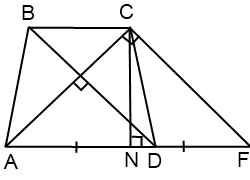
Четырехугольник BCFD — параллелограмм ( BC∥DF как основания трапеции, BD∥CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.

Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то

   $CN = \frac{1}{2}AF = \frac{{AD + BC}}{2},$

что в общем виде можно записать как

   $h = \frac{{a + b}}{2},$

где h — высота трапеции, a и b — ее основания.

2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.

Так как средняя линия трапеции m равна полусумме оснований, то

   $h = m.$

3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).

Так как площадь трапеции находится по формуле

   $S = \frac{{a + b}}{2} \cdot h$

а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:

   $h = \frac{{a + b}}{2} = m,$

то

   $S = {h^2}$

   $S = {(\frac{{a + b}}{2})^2}$

   $S = {m^2}.$

4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.

Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле

   $S = \frac{1}{2}{d_1}{d_2}\sin \varphi$

sin 90º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна

   $S = \frac{1}{2}{d^2}.$

откуда

   $\frac{1}{2}{d^2} = {(\frac{{a + b}}{2})^2} = {h^2} = {m^2},$

   ${d^2} = \frac{{{{(a + b)}^2}}}{2}.$

http://www.uznateshe.ru/

Метод интервалов для рациональных неравенств

Метод интервалов выручит! Избавит нас от рутины!

Мы ведь понимаем, что любое число – либо отрицательное (-), либо положительное (+), либо ноль. Где «переход» из одной зоны (+или — ) в другую (- или +)? В нуле!

На рисунке 1 функция обращается в нуль в точках -2; 1; 5 и 7. Именно при переходе через них она и меняет свой знак с одного на другой.

Функция может также коснуться оси (ох), и «не перескочить» в другую зону (как на рисунке 2). В данном случае точка $x=-2$ — корень четной кратности (мы еще поговорим об этом).

В любом случае, если функция попала из одной «зоны» («+,-») в другую («-,+»), — значит она в какой-то точке должна была обратиться в ноль.

Поэтому-то нули функции и помогут нам!

Итак, давайте выработаем алгоритм, которого будем придерживаться при решении рациональных неравенств.

Алгоритм решения рациональных неравенств

Пусть нам дано неравенство вида $f(x)\vee0$ , где $\vee$ — один из знаков $<,\leq,>,\geq$ .

1. Раскладываем $f(x)$ на множители (если это возможно*).

2. Находим нули $f(x)$ .

3. Отмечаем корни (нули) функции на оси в порядке возрастания. Эти числа разбивают числовую ось на интервалы. На каждом из этих интервалов выражение сохраняет знак, а, переходя через отмеченные точки, меняет знак на противоположный (или не меняет, если корень — четной кратности, например, в неравенстве $x^3(x-1)^4<0$ $x=1$ — корень четной кратности, корень $x=0$ — обычный).

4. Расставляем знаки на интервалах, начиная от крайнего правого.Советую брать «миллиончик» — не промахнетесь (шучу). Нам не важно само значение функции в выбранной точке, но только ЗНАК в ней, поэтому не утруждайте себя подсчетами - только грубая прикидка.

5. Выбираем подходящие нам промежутки, записываем ответ.Например, если неравенство со знаком «>», то берем интервалы со знаком «+», если неравенство со знаком «<», то берем интервалы со знаком «-», если неравенство со знаком $\leq$ ( $\geq$ ), то берем промежутки со знаком «+» («-») c закрытыми концами.

http://egemaximum.ru/

видео-урок по теме "Разложение квадратного трехчлена множители"
Видео-урок по теме "Теорема Виета"
Видео-урок по теме "Сложение и вычитание алгебраических дробей"
Применение ФСУ. Задания повышенного уровня сложности.
Видео-урок по теме "Квадрат суммы и квадрат разности"
Видео-урок по теме "Сложение и вычитание многочленов"
Видео-урок по теме "Одночлены и действия с ними"

Ребята, если возникают трудности в выполнении заданий домашней работы или если вы пропустили урок, то просмотрите видеоурок по теме "Умножение и деление степени с одинаковым показателем"

Для тех, кто пропустил или не понял тему "Свойства спенени с натуральным показателем". Посмотрите видео-урок, ребята. Надеюсь, что это вам поможет ВИДЕОУРОК
Здесь вы найдете комментарии по способам решения систем линейных уравнений.

Ребята, предлагаю вам видео-урок по теме "Линейная функция".Помните о том. что уравнение линейной функции может быть записано с использование разных букв латинского алфавита. В нашем учебнике оно выглядит так y=kx+m, а в этом видео-уроке y=kx+b. Мы это с вами обсуждали, надеюсь. Что затруднений не возникнет при просмотре урока.См. урок Оформление письменных работ по математике

Между классной и домашней работами следует отступать 4 клетки (на 5 клетке начинаем писать следующую работу).

Между видами работ в классной и домашней работах следует отступать 2 клетки (на 3 клетке пишем).

Между столбиками выражений, уравнений, равенств и т.п. отступаем 3 клетки вправо, на четвертой пишем.

Все номера заданий и задач, которые выполняются в тетрадях, необходимо записывать в тетрадь. Мы рекомендуем писать задания по середине строки либо на слева, т.к. это:

а) экономит место;

б) позволяет более четко и быстро найти номер задания при проверке любой работы, а отсюда более ясно просматривается структура классной или домашней работ.

Число можно писать на полях (например: 17.03.01 без буквы" г.").

Число на полях тоже пишется на пятой клетке по вертикали, т.е. на той же строчке, где и домашняя (классная) работа. В любой работе (классная или домашняя) слава по горизонтали отступаем одну клетку от края.

В письменной работе допускается и другая форма оформления. Перед каждым заданием учащиеся сами определяют цель задания и записывают ее в тетрадь.

Например: "Найти сумму";

"Найти вычитаемое";

"Найти значение выражения";

"Сравнить величины" и т.д.

Необходимо с первого класса оформлять поля с внешней стороны страницы тетради. На поля следует отводить четыре клетки. Поля проводить простым карандашом.

При записи математических выражений все символы (знаки, цифры) фиксируются с учетом правил каллиграфии, т.е. с соблюдением графики и соответствия количества клеток количеству записываемых символов. Особенно соблюдение этого требуется при работе с многозначными числами (сложение, вычитание, умножение, деление).

КАК ГОТОВИТЬ ДОМАШНИЕ ЗАДАНИЯ

ПАМЯТКА ДЛЯ УЧАЩИХСЯ

1. Активно работай на уроке: внимательно слушай, отвечай на вопросы.

2. Задавай вопросы, если чего-то не понял или с чем-то не согласен.

3. Точно и как можно подробнее записывай, что задано по каждому предмету.

4. Научись пользоваться словарями и справочниками. Выясняй значение незнакомых слов, находи нужные факты и объяснения, правила, формулы в справочниках.

5. Если у тебя есть компьютер, научись с его помощью находить нужную информацию, производить нужные расчеты с помощью электронных таблиц и т.п.

6. Если то, что проходили на уроке, показалось тебе трудным, повтори материал в тот же день, даже если следующий урок будет через несколько дней.

7. Приступая к выполнению каждого задания, думай не только о том, что надо сделать (то есть о содержании задания), но и о том, как (с помощью каких приемов, средств) это можно сделать.

8. В случае необходимости обращайся за помощью ко взрослым или к одноклассникам.

9. Приступая к выполнению уроков, раскрой дневник, посмотри, все ли задания записаны.

10. Продумай последовательность выполнения заданий по отдельным предметам и прикинь, сколько времени тебе понадобится для выполнения каждого задания.

11. Убери со стола все лишнее — то, что может отвлекать. Приготовь то, что нужно для выполнения первого задания (учебник, тетради, карты, карандаши, словари, справочники и т.п.). После того как подготовишься к первому уроку, все убери и приготовь то, что нужно для выполнения следующего, и т.п.

12. Между уроками делай перерывы.

13. Сначала постарайся понять материал, а затем его запомнить.

14. Прежде чем выполнять письменные задания, пойми и выучи правила, на которые оно направлено.

15. При чтении параграфа учебника задавай себе вопросы: о чем или о ком говорится в этом тексте, что об этом говорится.

16. Ищи связь каждого нового понятия, явления, о котором ты узнаешь, с тем, что ты уже знаешь. Соотноси новое с уже известным. Следи за тем, чтобы это были не случайные, внешние связи, а главные связи, связи по смыслу.

17. Если материал, который надо выучить, очень большой или трудный, разбей его на отдельные части и прорабатывай каждую часть в отдельности. Используй метод ключевых слов. 18. Не оставляй подготовку к докладам, сочинениям, творческим работам на последний день, поскольку это требует большого количества времени. Готовься к ним заранее, на протяжении нескольких дней, распределяя нагрузку равномерно.

19. При подготовке устных уроков используй карты, схемы. Они помогут тебе лучше понять и запомнить материал. К ним необходимо обращаться и при ответах на уроке. Чем лучше ты умеешь пользоваться картами, схемами, таблицами, тем выше будет оценка.

20. Попробуй использовать при подготовке устных заданий метод «5 П», разработанный американскими психологами. По данным психологов США, такой метод позволяет сосредоточить внимание на самом важном в тексте и способствует лучшему его запоминанию.

21. Составляй план устного ответа.

22. Проверяй себя. У тебя все получится! Помни: мы лучше всего запоминаем: — то, чем постоянно пользуемся;

— то, к чему нам надо будет вернуться (прерванные действия);

— то, что нам нужно;

— то, что мы можем связать с другими нашими знаниями и умениями;

— то, что связано с нашими переживаниями (и приятными, и неприятными).

МЕТОД КЛЮЧЕВЫХ СЛОВ

Ключевые слова — самые важные в каждом абзаце.

Ключевое слово должно способствовать воспроизведению соответствующего абзаца. Вспоминая ключевые слова, мы сразу вспоминаем весь абзац.

Читая абзац, выбери для него одно-два ключевых слова.

После выбора ключевых слов запиши их в той последовательности, которая нужна для выполнения задания.

К каждому ключевому слову поставь вопрос, который позволит понять, как оно связано с соответствующим разделом текста. Обдумай и постарайся понять эту взаимосвязь.

Соедини два соседних ключевых слова с помощью вопросов.

После соединения каждого ключевого слова со своим разделом текста и с последующим ключевым словом образуется цепочка.

Запиши эту цепочку и постарайся ее выучить.

Перескажи текст, опираясь на эту цепочку.

МЕТОД «5 П»

1 П — Просмотри текст (бегло)

2 П — Придумай к нему вопросы

3 П — Пометь карандашом самые важные места

4 П — Перескажи текст

5 П — Просмотри текст повторно

Омега

Достижения учеников

В помощь ученику

Метод интервалов для рациональных неравенств

Алгоритм решения рациональных неравенств

КАК ГОТОВИТЬ ДОМАШНИЕ ЗАДАНИЯ

Комментариев нет:

Отправить комментарий