Тесты ОГЭ (ГИА) 2015 онлайн
Демоверсии тестов ГИА 2015 доступны онлайн. Тесты ГИА 2015 онлайн по математике, русскому языку и другим предметам (физика, обществознание, история, химия, биология, информатика, география, литература, иностранный язык). Официальные демонстрационные материалы ГИА 2015 с ответами. ЗДЕСЬ
Демоверсия ГИА 2015 по математике
Демоверсия содержит 20 вопросов. Обратите внимание: в строку ответа номера правильных ответов необходимо записывать без пробелов и знаков препинания. Дробные числа необходимо записывать через точку, например, 2.5.
9/02/15 на последней консультации по подготовке ОГЭ рассматривали виды заданий, которые встречаются в задании 21. Предлагаю видеоуроки по этому заданию посмотреть здесь. Обязательно отвечу на вопросы, если они у вас возникнут, ребята. Совет - прорешивайте с карандашом в руках, делайте пометки в тех местах, где у вас возникают сомнения или вы что-то не поняли.
- Решение заданий 23 смотрите здесь
- Решение заданий 24 (геометрия) здесь
- Решения заданий 25 (геометрия) здесь
Видео уроки по части 2 ОГЭ по математике смотрите ЗДЕСЬ
Шкала перевода баллов по МАТЕМАТИКЕ
Максимальный первичный балл: 38 балла (увеличился на 5 балла). Из них – за модуль «Алгебра» – 17 баллов, за модуль «Геометрия» – 14 баллов, за модуль «Реальная математика» – 7 баллов.
Минимальный порог: 8 баллов (из них не менее 3 баллов по модулю «Алгебра», не менее 2 баллов по модулю «Геометрия» и не менее 2 баллов по модулю «Реальная математика»)
Преодоление этого минимального результата даёт выпускнику право на получение, в соответствии с учебным планом образовательного учреждения, итоговой оценки по математике (если изучение математики осуществлялось выпускником в рамках интегрированного курса математики) или по алгебре и геометрии.
Шкала пересчёта первичного балла за выполнение экзаменационной работы в целом в отметку по математике:
Отметка по
пятибалльной шкале
|
«2»
|
«3»
|
«4»
|
«5»
|
Общий балл
|
0 – 7
|
8 – 15
|
16 – 22
|
23 – 38
|
Шкала пересчёта первичного балла за выполнение модуля «Алгебра» в отметку по алгебре:
Отметка по
пятибалльной шкале
|
«2»
|
«3»
|
«4»
|
«5»
|
Общий балл
|
0 – 5
|
6 – 11
|
12 – 16
|
17 – 23
|
Шкала пересчёта первичного балла за выполнение модуля «Геометрия» в отметку по геометрии:
Отметка по
пятибалльной шкале
|
«2»
|
«3»
|
«4»
|
«5»
|
Общий балл
|
0 – 2
|
3 – 4
|
5 – 8
|
9 – 15
|
Результаты экзамена могут быть использованы при приеме учащихся в профильные классы средней школы. Ориентиром при отборе в профильные классы может быть показатель, нижняя граница которого соответствует 18 баллам.
- 15/12/14 прошел зачет по математике в формате ОГЭ. Все участники смогли попробовать свои силы, почувствовать атмосферу будущего экзамена. Знаю, что кто-то из вас остался доволен своим результатом, кто- то - ни очень, а кто-то очень огорчился. Но я не устаю повторять, что все в ваших руках, что количество затраченных усилий (временных, умственных, эмоциональных и др.) обязательно перерастет в качество. И этому есть немало подтверждений. Посмотреть ответы к вашим вариантам вы можете здесь. Выбирайте номер своего варианта, один из файлов будет с ответами. Проверьте себя, ребята, если что-то будет непонятно - я помогу. Индивидуально по работам вашим можно будет встретиться 22.12.14 с 13.00 каб. 60. Консультация по части 2 будет 22.12.14 в 14.00 как обычно. Тема консультации "Функции. Графики функций" (модули, параметры)
- Ребята здесь можете познакомиться в инструкцией по заполнению бланков ОГЭ по математике и увидеть бланки.
- Ребята, предлагаю в качестве тренажера по %%% пройти тест онлайн ЗДЕСЬ. Затем обсудим что и как.
- Задачи на сложные проценты для консультации 1.12.14
1.За первый год предприятие увеличило
выпуск продукции на 8%, в следующем году выпуск увеличился на 25%. На сколько
процентов вырос выпуск продукции по сравнению с первоначальной?
2Вследствие инфляции
цены выросли на 150%. Дума потребовала от правительства возвращение цен к
прежнему уровню. Для этого цены должны быть уменьшены (на сколько процентов)?
3.Тетрадь
стоит 40 рублей. Какое наибольшее количество таких тетрадей можно купить на 650
рублей, после понижения на 15%?
4.Сколько граммов воды
надо добавить к 50г раствора, содержащего 8% соли, чтобы получить 5% раствор?
5.Свежие грибы по массе
содержат 90% воды, а сухие 12%. Сколько получится сухих грибов из 22 кг свежих?
6.Вкладчик открыл счет
в банке, внеся 2000 рублей на вклад, годовой доход по которому составляет 12%,
и решил в течение шести лет не брать процентные начисления. Какая сумма будет
лежать на счете через шесть лет?
7.После двух
последовательных снижений цен на одно и то же число процентов стоимость товара
с 400 рублей снизилась до 324 рублей. На сколько процентов стоимость товара
снижалась каждый раз?
8.По пенсионному
вкладу банк выплачивает 12% годовых. По истечению каждого года эти проценты
капитализируются, то есть начисленная сумма присоединяется к вкладу. На данный
вид вклада был открыт счет на 80000 рублей, который не пополнялся и с которого
не снимались деньги в течении двух лет. Какой доход был получен по истечении
этого срока?
9.Банк предлагает
клиентам два вида вкладов. Первый «До востребования» со следующим порядком
начисления процентов: каждые 6 месяцев счет увеличивается на 10% от суммы,
имеющиеся на счету клиента в момент начисления. Второй вклад «номерной» с
ежегодным начислением процентов по вкладу. Сколько процентов годовых должен
начислять банк по второму вкладу, чтобы равные суммы, положенные клиентом на
каждые из указанных счетов, через два года оказались снова равными?
10. Для определения
оптимального режима снижения цен социологи предложили фирме с первого января
снижать цены на товар в двух магазинах двумя способами. В одном магазине – в
начале каждого месяца (начиная с февраля) на 20%, в другом через каждые два месяца,
в начале третьего (начиная с марта) на одно и тоже число процентов, причем
такое, чтобы через полгода (первого июля) цены снова стали одинаковыми. На
сколько процентов надо снижать ценны товара через каждые два месяца во втором
магазине?
___________________________________________________________________________
Задача 1. После открытия торгов на бирже в понедельник акции некой
компании выросли в цене на неизвестное количество процентов. А во вторник на то
же самое количество процентов упали в цене. В итоге они подешевели на 4% по
отношению к своей первоначальной стоимости в понедельник. На какой процент
акции этой компании поднимались в цене в понедельник?
Задача 2. Четыре пары брюк дешевле одного пальто на 8%. Подсчитайте,
на сколько процентов пять пар брюк стоят дороже, чем одно пальто.
Семья состоит из трех человек: муж, жена и
дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи
возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой
семьи уменьшится на 4%. Надо вычислить, какой процент в общий доход семьи
приносит заработок жены.
Задача 4. В емкости находится 5 литров водного раствора с
концентраций вещества, равной 12%. В емкость добавили еще 7 литров воды.
Раствор какой концентрации (с каким процентным содержанием вещества) получился
после этого?
Задача 5. В свежих абрикосах 90% влаги, а в кураге, которая из них
получается, только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20
килограммов кураги?
ОТВЕТЫ к задачам 1-5
Задача 1. После открытия торгов на бирже в понедельник акции некой
компании выросли в цене на неизвестное количество процентов. А во вторник на то
же самое количество процентов упали в цене. В итоге они подешевели на 4% по
отношению к своей первоначальной стоимости в понедельник. На какой процент
акции этой компании поднимались в цене в понедельник?
Решение. Пускай первоначальная стоимость акций это 1. В понедельник
акции дорожают на х * 100%. Их стоимость в это время: 1 + х * 1. Во вторник
акции дешевеют на х * 100%. Их стоимость после этого: 1 + х – х * (1 + х).
После чего они стали дешевле на 4%, т.е. стали стоить 0,96.
Отсюда
1 + х – х * (1 + х) = 0,96 ↔1 – х2 = 0,96 ↔ х2 =
0,04 ↔ х = 0,2. Т.е. в понедельник акции компании дорожали на 20%.
Задача 2. Четыре пары брюк дешевле одного пальто на 8%. Подсчитайте,
на сколько процентов пять пар брюк стоят дороже, чем одно пальто.
Решение. Исходя из условия задачи, стоимость четырех пар брюк – это
92% от стоимости пальто. Легко подсчитать, что стоимость одной пары брюк – это
23% стоимости пальто (92/4 = 23). Теперь умножим стоимость одной пары брюк на
пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто (23 * 5 =
115). Т.е. пять пар брюк на 15% дороже, чем одно пальто.
Задача 3. Семья состоит из трех человек: муж, жена и дочь-студентка.
Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%.
Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на
4%. Надо вычислить, какой процент в общий доход семьи приносит заработок жены.
Решение. Из условия следует, что общий доход семьи находится в
прямой зависимости от доходов мужа. Не так важно, насколько ему поднимут
зарплату. В любом случае общий доход семьи вырастет на 67%. Значит, зарплата
мужа составляет как раз эти 67% от общего дохода. Если стипендия дочери
уменьшится в три раза (т.е. на 1/3), останется 2/3 – это и есть 4%, на которые
уменьшился бы семейных доход. Можно составить простую пропорцию и выяснить, что
раз 2/3 стипендии – это 4% дохода, то вся стипендия – это 6%. А теперь отнимем
от всего дохода вклад мужа и дочери и узнаем, какой процент составляет
заработок жены в общем доходе семьи: 100% – 67% – 6% = 27%.
Задача 4. В емкости находится 5 литров водного раствора с
концентраций вещества, равной 12%. В емкость добавили еще 7 литров воды.
Раствор какой концентрации (с каким процентным содержанием вещества) получился
после этого?
Решение. Опишем концентрацию вещества в растворе такой формулой: С
= Vвещества/ Vраствора * 100%. Изначально в растворе содержится 0,12 * 5 = 0,6
литра вещества. Когда были добавлены 7 литров воды, объем раствора в емкости
увеличился. Но концентрация вещества понизилась (его объем остался неизменным).
Подставим все известные нам цифры в формулу и получим ответ: 0,6/5 + 7 *100% =
0,6 /12 * 100% = 5%.
Задача 5. В свежих абрикосах 90% влаги, а в кураге, которая из них
получается, только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20
килограммов кураги?
Решение. Исходя из условия, в абрикосах 10% питательного вещества,
а в кураге оно содержится в концентрированном виде – 95%. Поэтому в 20
килограммах кураги 20 * 0,95 = 19 кг питательного вещества. На вопрос задачи мы
ответим, если разделим одинаковое количество питательного вещества, которое
содержится в разных объемах свежих абрикосов и кураги, на его процентное
содержание в абрикосах. Чтобы получить 20 килограммов кураги, нужно взять
19/0,1 = 190 килограммов свежих абрикосов.
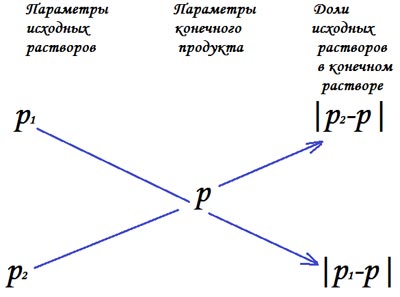
- Старинный способ решения задач на смеси, сплавы и растворы (правило креста)
Впервые о нем было упомянуто в первом печатном учебнике математики Леонтия Магницкого.
Данный способ применялся купцами и ремесленниками при решении различных практических задач. Но в задачниках и различных руководствах для мастеров и торговцев никаких обоснований и разъяснений не приводилось. Просто давался рецепт решения: либо рисовалась схема, либо словесно описывалась последовательность действий — поступай так и получишь ответ.
Задача 5.
Один раствор содержит 20 % соли, а второй – 70 %. Сколько граммов первого и второго раствора нужно взять, чтобы получить 100 г 50% раствора.
Решение:
Применим правило “креста”.
Составим схему:
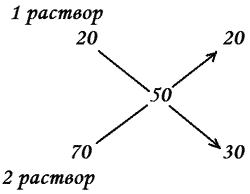
Значит, 100 г смеси составляют 20 + 30 = 50 частей.
100 : ( 20 + 30 ) = 2 г - на 1 часть.
2 * 20 = 40 г – 20% раствора
2 * 30 = 60 г – 70 % раствора
Ответ: 40 г- 20 % раствора; 60 г- 70 % раствора.
Задача 6.
Первый сплав содержит 10 % меди, второй - 25 % меди. Из этих двух сплавов получили третий сплав массой 30 кг, содержащий 20 % меди. Какое количество каждого сплава было использовано?
Решить задачу разными способами: системой уравнений, линейным уравнением, “крестом”.
(по рядам.)
1 способ: (система уравнений)
| % содержания вещества | Масса сплава | Масса меди | |
| 1 сплав | 10% = 0,1 | Х кг | х * 0,1 |
| 2 сплав | 25% = 0,25 | У кг | у * 0,25 |
| сплав | 20 % = 0,2 | 3 кг | 3 * 0,2 |
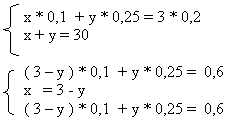
0,15 у = 0,3 у = 2 , значит х = 1.
Ответ: 1 сплав – 1 кг, 2 сплав – 2 кг.
2 способ: ( линейное уравнение)
| % содержания вещества | Масса сплава | Масса меди | |
| 1 сплав | 10% = 0,1 | Х кг | х * 0,1 |
| 2 сплав | 25% = 0,25 | 3 - х кг | ( 3 – х) * 0,25 |
| сплав | 20 % = 0,2 | 3 кг | 3 * 0,2 |
х * 0,1 + ( 3 - х ) * 0,25 = 3 * 0,2
х * 0,1 + 0,75 - х * 0,25 = 0,6
- 0,15 х = - 0,15
х = 1, значит 3 – 1 = 2.
Ответ : 1 сплав – 1 кг, 2 сплав – 2 кг.
3 способ: (“крест”)
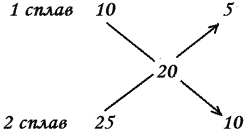
5+10 = 15 частей в 3 кг
3: 15 = 0,2 кг – в 1 части.
На 5 частей – 0,2 * 5 = 1 кг
На 10 частей - 0, 2 * 10 = 2 кг
Ответ: 1 сплав – 1 кг, 2 сплав – 2 кг.
http://festival.1september.ru/articles/644729/
http://festival.1september.ru/articles/644729/
.jpg)
.jpg)
Комментариев нет:
Отправить комментарий